Dernière modification: 07/08/2023
Le taux de défaillance est la base de la théorie de la sécurité fonctionnelle.
[IEC 61508-4] 3.6 Défaut, défaillance et erreur
3.6.16 Taux de défaillance. Paramètre de fiabilité λ(t) d’une entité (composants individuels ou systèmes) tel que λ(t)dt est la probabilité de défaillance de cette entité au cours de [t, t+dt] à condition qu’elle ne soit pas tombée en panne au cours de [0, t].
Mathématiquement, λ(t) est la probabilité conditionnelle de défaillance par unité de temps sur [t, t+dt]. Il est possible de démontrer que le taux de défaillance instantané est :
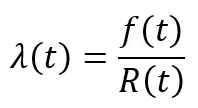
En utilisant l’équation , il est possible d’obtenir :
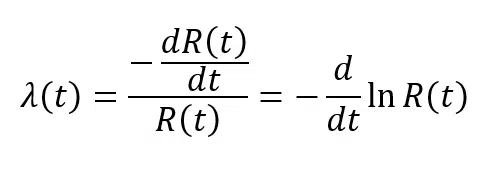
Intégration de l’équation supérieure dans le temps :
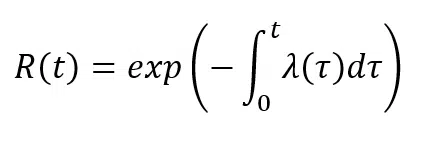

Les taux de défaillance et leurs incertitudes peuvent être estimés à partir du retour d’expérience sur le terrain, en utilisant des statistiques conventionnelles.
Le modèle le plus diffus et le plus connu pour le taux de défaillance est la courbe « en baignoire ». Dans la phase initiale de la durée de vie du composant, λ(t) diminue rapidement avec le temps ; ce fait découle de l’existence d’une fraction « faible » de la population dont les défauts provoquent une défaillance dans un court laps de temps à partir du moment où ils sont produits.

Dans la période dite de vie utile, λ(t) est approximativement constant, dans le cas, par exemple, des composants électroniques. Pour les composants électromécaniques, λ(t) est fonction du temps et, dans cet intervalle, il augmente constamment.
La dernière période est caractérisée par une usure, avec un taux de défaillance λ(t) qui augmente rapidement en raison de l’usure, du vieillissement et de la fatigue.
Pendant la durée de vie utile d’un composant avec un taux de défaillance constant, en considérant comme condition initiale que la fiabilité au temps 0 est maximale et égale à 1, nous avons :
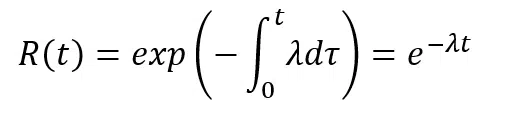
La fonction de fiabilité R(t) est représentée à la figure 2a et les fonctions de densité de probabilité f(t) à la figure 2b, dans le cas où λ = constant.
Le tableau 1 présente un résumé des quatre fonctions décrites jusqu’à présent.

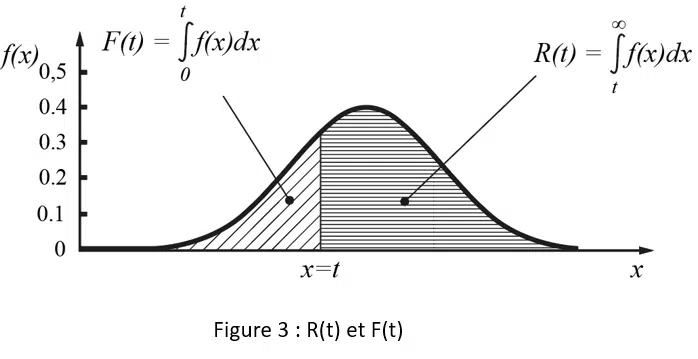
La figure 3 montre la relation entre F(t) et R(t).