Ultima modifica: 09/01/2024
Il tasso di guasto è la base delle teoria sulla Sicurezza Funzionale.
[IEC 61508-4] 3.6 Fault, failure and error
3.6.16 Failure rate. Reliability parameter λ(t) of an entity (single components or systems) such that λ(t)dt is the probability of failure of this entity within [t, t+dt] provided that it has not failed during [0, t].
Matematicamente, λ(t) è la probabilità condizionata di guasto per unità di tempo su [t, t+dt]. È possibile dimostrare che il tasso di guasto istantaneo è:
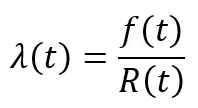
Utilizzando l’equazione , è possibile ottenere:
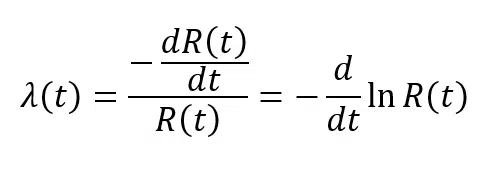
Integrando l’equazione precedente nel tempo:
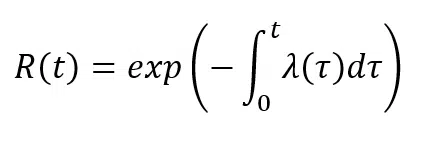
I tassi di guasto e le loro incertezze possono essere stimati dai riscontri sul campo, utilizzando le statistiche convenzionali.
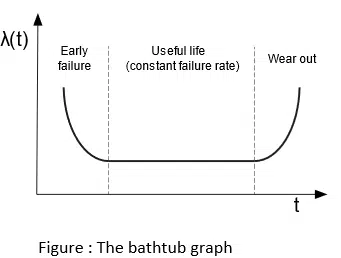
Il modello più diffuso e conosciuto per il tasso di guasto è la curva a “vasca da bagno“. Nella fase iniziale della vita del componente, λ(t) diminuisce rapidamente con il tempo; questo fatto deriva dall’esistenza di una frazione “debole” della popolazione i cui difetti causano un guasto entro un breve periodo di tempo dal momento della produzione.
Nel periodo chiamato vita utile, λ(t) è approssimativamente costante, ad esempio nel caso di componenti elettronici. Per i componenti elettromeccanici, λ(t) è una funzione del tempo e, in questo intervallo, aumenta costantemente.
L’ultimo periodo è caratterizzato da un’usura, con un tasso di guasto λ(t) in rapido aumento a causa dell’usura, dell’invecchiamento e della fatica.
Durante la vita utile di un componente con un tasso di guasto costante, considerando come condizione iniziale che l’affidabilità al tempo 0 sia massima e pari a 1, si ha:
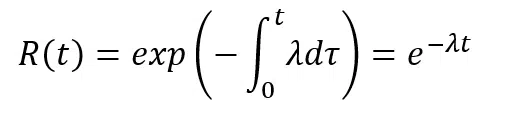
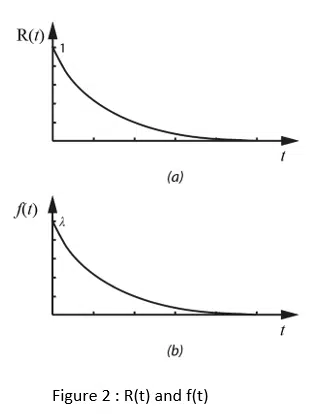
La funzione di affidabilità R(t) è mostrata nella Figura 2a e le funzioni di densità di probabilità f(t) nella Figura 2b, nel caso λ = costante.
La Tabella 1 mostra una sintesi delle quattro funzioni descritte finora.

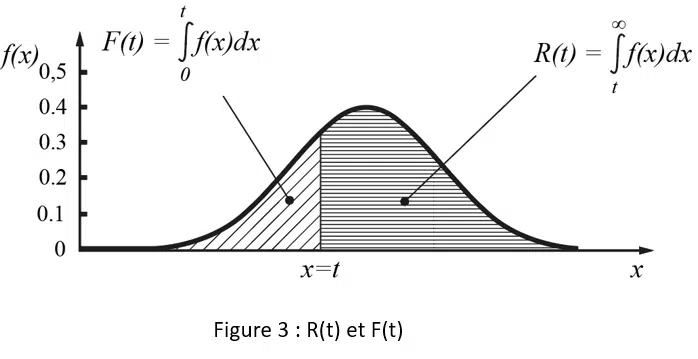
La figura 3 mostra la relazione tra F(t) e R(t)